In Regression Analysis the Unbiased Estimate of the Variance Is
In regression analysis the unbiased estimate of the variance is a. Coefficient of correlation b.

Two Stage Least Squares 2sls Regression Analysis Statistics Solutions
Note that RSS there stands for residual sum of squares.

. Question 15 3 points In regression analysis the unbiased estimate of the variance is mean square error. β 0 and β 1. Coefficient of determination c.
The most common form of regression analysis is linear regression in which one. Mean square error d. The variance-covariance matrix of the regression models errors is used to determine whether the models error terms are homoskedastic constant variance and uncorrelated.
In statistics and in particular statistical theory unbiased estimation of a standard deviation is the calculation from a statistical sample of an estimated value of the standard deviation of a population of values in such a way that the expected value of the calculation equals the true value. The subtraction of 2 can be thought of as the fact that we have estimated two parameters. 1017850120130324 Unbiased Estimation of Moment Magnitude from Body- and Surface-Wave Magnitudes by Ranjit Das H.
Slope of the regression equation ANS. It can be shown that the third estimator y_bar the average of n values provides an unbiased estimate of the population mean. Square root of the coefficient of.
So just as with sample variances in univariate samples reducing the denominator can make the value correct on average. In statistical modeling regression analysis is a set of statistical processes for estimating the relationships between a dependent variable often called the outcome or response variable and one or more independent variables often called predictors covariates explanatory variables or features. Slope of the regression equation.
A simple linear regression model in which the slope is zero vs. N p 1 σ 2 σ 2 χ N p 1 2. Difference between the actual y values and their predicted values B.
Total variation in the response is expressed by the deviations. The unbiased estimate of the error variance σ 2is s MSE SSE n2 where MSE is the Mean Square Error. In summary we have shown that if X_i is a normally distributed random variable with mean mu and variance sigma2 then S2 is an unbiased estimator of sigma2.
In any case this is probably a good point to understand a bit more about the concept of bias. Coefficient of determination c. But then so do the first two.
Statistics and Probability questions and answers. σ 2 1 N p 1 i 1 N y i y i 2. Analysis of variance summarizes information about the sources of variation in the data.
Topic 4 - Analysis of Variance Approach to Regression STAT 525 - Fall 2013 STAT 525 Outline Partitioning sums of squares Degrees of freedom Expected mean squares General linear test R2 and the coefficient of correlation. Sometimes SSE - sums of squares of error - is used instead. The variance-covariance matrix of the fitted regression models coefficients is used to derive the standard errors and confidence intervals of the fitted models coefficient estimates.
A simple linear regression model in which the slope is not zero. Except in some important situations outlined later the task has little relevance to. Apparently an unbiased estimator of the variance σ 2 is given by.
Y 408 0766 X. Which estimator should we use. That is s 2 n n p s n 2 R S S n p 1 n p i 1 n y i y i 2.
For both models it is assumed that independent. In regression analysis the residuals represent the. In regression analysis the unbiased estimate of the variance is a.
In regression analysis the unbiased estimate of the variance is. Regression Analysis The regression equation is. Bulletin of the Seismological Society of America Vol.
The rationale is simple and proceeds as follows. If one expects to obtain an accurate estimate of the variance through modeling it is pertinent that the right data be used to do the modeling. Slope of the regression equation.
18021811 August 2014 doi. It turns out however that S2 is always an unbiased estimator of sigma2 that is for any model not just the normal model. Difference between the actual x values and their predicted values C.
Or the residual sum of squares divided by the degrees of freedom. Estimate 3 of the population mean1194113359335031. Statistics and Probability questions and answers.
The estimators βˆ 1 and βˆ 0 are linear functions of Y 1Y n and thus using basic rules of mathematical. I have to show that the variance estimator of a linear regression is unbiased or simply Eleftwidehatsigma2rightsigma2. Im familiar with Bessels Correction but I still couldnt reconcile these two.
In regression analysis the unbiased estimate of the variance is. Acoefficient of correlationbcoefficient of determinationcmean square errordslope of the regression equation. Sharma Abstract For regression of variables having measurement errors general orthogonal regression GOR is the most.
Thus we have arrived at the following unbiased estimate of the variance-covariance matrix of the coefficients of the fitted OLS regression model. In normal theory regression the function of the means model residuals that is generally agreed to yield an appropriate response for variance modeling is T eewls i e 2 ewls i. In regression analysis the things to remember about a matrixs inverse are the following.
Question 13 3 points In regression analysis the unbiased estimate of the variance is slope of the regression equation. The interval estimate of the mean value of y for a given value of x is. If β1 0 MSR unbiased estimate of.
Coefficient of correlation b. The inverse of X is denoted as X-1. I have seen a few similar questions on here but I think they are different enough to not answer my question.
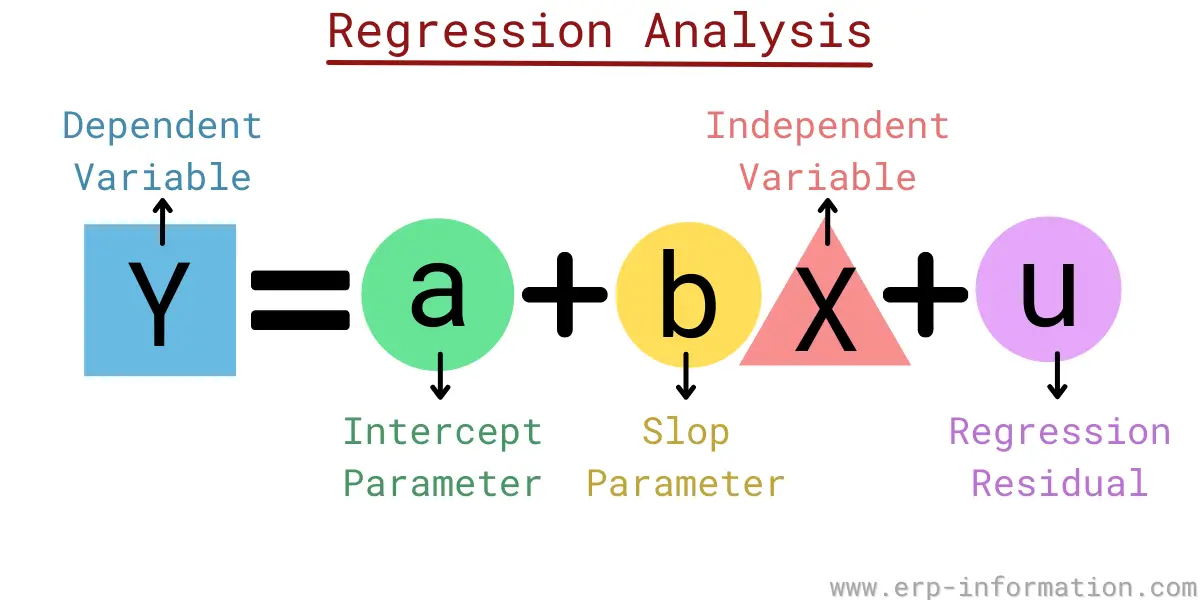
What Is Regression Analysis Types Of Regression Analysis

Multicollinearity In Regression Analysis Problems Detection And Solutions Statistics By Jim
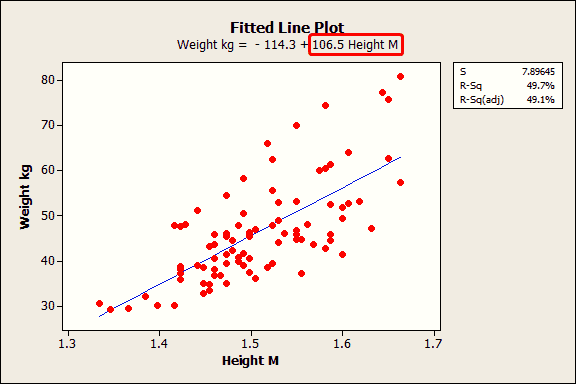
How To Interpret P Values And Coefficients In Regression Analysis Statistics By Jim
No comments for "In Regression Analysis the Unbiased Estimate of the Variance Is"
Post a Comment